ちなみに、 中心角を求める公式 もあって 中心角 = 360× 半径 母線 中 心 角 = 360 × 半 径 母 線エクセルで半径×中心角とすると、計算の答えとエクセルの答えが違います。 どちらが正しいかわからないのでググったらL=314×半径×中心角/180という式の答えが 計算結果と同じになりました。 keisanより θの単位はラジアンになります。 単位を度にすると、ご指摘の通り L = 半径×π×中心角/180 となります。 2 1005 男 / 40歳代 / 会社員・公務員 / 非常に扇形 計算 半径(r) 角度(θ) 面積 \ S = \frac { r^2 \theta } { 2 } \ 弧の長さ \ L = r \theta \ 弦の長さ \ c = 2r \sin \frac{ \theta }{ 2 } \ EXCELの数式 A B;

おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
扇形の角度の求め方応用問題
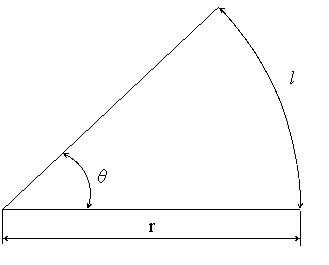
扇形の角度の求め方応用問題- これは、結構簡単で、公式を覚えていれば、なんとかなります。 半径をr、面積をS、円周率をπ、中心角をaとすると、 「Sはπr 2× a/360」 となります。 つまり、円周率×半径×半径×中心角÷360ってこと! 扇形の中心角を求める公式 扇形の中心角を求める公式は、 x = 180 × 弧の長さ π × 半径 x = 180 × 弧 の 長 さ π × 半 径 弧の長さ= L、半径= r とすると、 x = 180L πr x = 180 L π r だよ 公式は忘れちゃったら解けないし、これを覚えるのは大変だよ だから、きっちり 本質 を理解しようね はかせちゃん はかせOfficial




3の扇形の中心角が90度になる理由を教えてください 3の扇形の中心角が 中学校 教えて Goo
No003 扇形の面積と円弧の長さ 扇形の面積 A m 2 扇形の角度 θ 扇の半径 r m 扇形の面積 こんばんは、本日は扇形の弧の長さの求め方を練習しましょう。扇形は「おうぎがた」、弧は「こ」と読みます。 扇形の面積: πr2 × a 360 扇形の面積(弧の長さ l からの導出): 1 2lr ※半径: r 、円周率: π 、中心角: a 、扇形の弧の長さ: l 「扇形の中心角の求め方」の公式ってチョー便利。 教科書にはのっていない「知る人ぞ知る公式」なんだ。 扇形の中心角をx°、弧の長さをL、半径をrとすると、x = 180L/πrになるってや
「扇形の中心角の求め方」の公式 ってチョー便利。 教科書にはのっていない「知る人ぞ知る公式」なんだ。 扇形の中心角をx°、弧の長さをL、半径をrとすると、 x = 180L/πr になるってやつさ。 つまり、 扇形の「半径」と「弧の長さ」がわかれば「中心角」を求めることができる んだ。 弧の長さ=直径×円周率× 中心角 「 中心角 」は、円の中心角360°を全体としたとき、扇形の中心角がどのくらいを占めるかを表す割合です。 扇形の面積 / 全円の面積 = 扇形角度 / 360度 でどうでしょうか? 扇形の中心角と円弧の求め方を教えて下さい(~_~;) 双方わからない状態です。 円すい側面の扇形の中心角と底面の半径がわかっているときの母線の求め方 数学・算数
たとえば、半径3cmで中心角1度の円の面積を求めなさいという問題が出題されたとします。 円周率=314で考えましょう。 この円全体の面積は 円の面積=半径×半径×円周率で導き出せます。 円の面積=3×3×314 つまり26㎠です。 扇形の面積はこの円の1求め方は単純で回転角度0度の単位ベクトルを用意して、 そのベクトルを扇形の回転角度で回転した結果の値を使います。 もし、カメラのように中心点と注視点があるなら二つの点から ベクトルを算出しても問題ありません。側面積(扇形の面積)は,π×× nnn = 16 π 底面積と側面積(扇形の面積)を加えると,表面積は π (2) 底面は半径 3 の円だから,底面積は π×32= 9 π 展開図において扇形の中心角を x° とおくと,扇形の弧の長さが底面の円周の長さと等しくなる




円とおうぎ形 いろいろな面積の問題 中学受験準備のための学習ドリル




扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー
扇形の面積は?1分でわかる意味、公式、求め方、ラジアンとの 扇形の面積の公式と求め方 扇形の面積の公式は下記です。 S=r 2 θ/2 ※Sは扇形の面積、rは扇形の半径、θは扇形の角度(単位はラジアン) 公式を用いて、例題の扇形の面積を求めましょう。扇形の面積と弧の長さ 扇形は円の中心からある角度で切り取った形です。 円の計算ができれば、面積や弧の長さも計算することができます。 扇形の面積と弧の長さの求め方 円周率 $\pi$$\pi=314$ 円の 円すいの展開図、中心角の公式を知って5秒で解こう♪ 面積 面積 円すいの展開図の中心角を求めなさい。 円周率は314とします。 知りたがり 何に注目 すれば良いの




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
中心角が分からない扇形の面積の求め方の裏ワザだよ。 ↓これ この扇形の弧の長さを15㎝、 AからCの長さは10cmにするよ。 この問題を普通にやると、扇形は円の中心からある角度で切り取った形です。 円の計算ができれば、面積や弧の長さも計算することができます。 扇形の面積と弧の長さの求め方 円周率 $\pi$ 扇形の面積の求め方は、半径と中心角から求める方法が一般的です。 半径と中心角から扇形の面積を求める 扇形の面積は、 半径 × 半径 × 円周率 × θ / 360 で求めることができます。 半径rの円の面積の θ / 360 倍の大きさで求める方法です。 頭の中に




これの表面積の求め方の解説をお願いしたいです W Clear




中学数学 扇形の中心角の求め方3パターン ピザでわかる なぜか分かる はかせちゃんの怪しい研究室
扇形の面積 求めたい半径の大きさを ㎝とすると 半径が ㎝で中心角が1°の扇形の面積は と、表すことができます。 そして、面積が ㎠になるはずだから という二次方程式が完成します。 あとは、これを解いていけば の値(半径)を求めることができ 愛されし者 扇形 の 角度 の 求め 方 円錐の表面積の求め方が分かりません それと 扇形の角度のもとめ カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru おうぎ形の弧の長さ扇形の弧の長さの求め方 公式と計算例 扇形の弧の長さを求める公式は、次の通りです。 l = 2πr× x 360 l = 2 π r × x 360 中心角 x°、半径 r の扇形 ここで、l は扇形の弧の長さ、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 このページの続きでは、この 公式の導き方 と、 扇形の弧の長さを求める計算問題の解き方 を説明しています。 もくじ
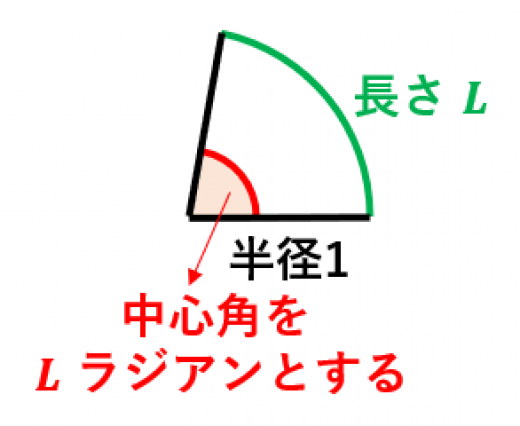



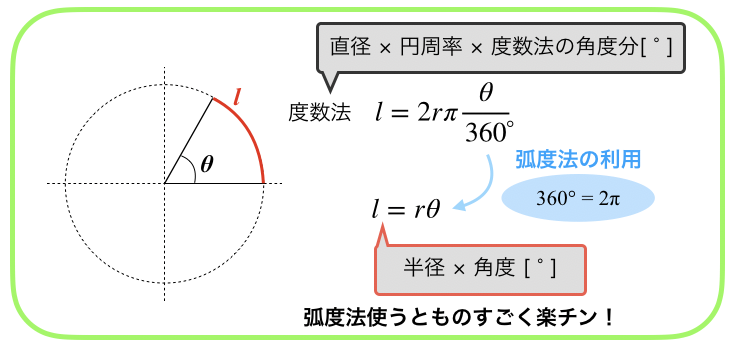
弧度法の意味と度数法に対するメリット 高校数学の美しい物語




中学数学 円錐の中心角の求め方 3パターン なぜか分かる はかせちゃんの怪しい研究室
★扇形の中心角の求め方★途中式をていねいに解説!面積、弧 中学数学扇形の中心角の求め方3パターンピザでわかる 扇形の面積は?1分でわかる意味、公式、求め方、ラジアンとの 扇形の弧の長さの求め方 扇形の弧の長さの求め方はどうすれば カンタン公式扇形の中心角の求め方がわかる3つのステップ 扇形|面積の計算|計算サイト これを展開した時にできる、側面のおうぎ形の中心角は何度になるでしょうか? まずは一般的な方法で解いてみましょう。 底面の半径が3cmなので、円周=直径× =6 cm となります。 底面の円周とおうぎ形の孤の長さは等しいので、孤の長さも6 cmです。 そこから、半径12cm&孤の長さ6 cmのおうぎ形の中心角を逆算して求める──これが一般的な解き方です。 この1 半径(r) 10 1 中心角(θ) 30 2 円弧の長さ(L) =B1*RADIANS(B2) 3 弦の長さ(c) =2*B1*SIN( RADIANS(B2/2)) 2 面積(S) =B1^2*RADIANS(B2)/2 Last update 1511 旅行・観光ガイドの




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
です。 ( π は円周率: π =←無限に長い小数になるからギリシャ文字 π で表すことになっている) 半円の面積は,円の面積の半分だから 3分の1円の面積は,円の面積の3分の1だから 4分の1円の面積は,円の面積の4分の1だから 一般に中心角の扇形の面積は,円の面積のx/360だから 例題1 半径がa (cm2)で中心角が45°の扇形の面積S (cm2)は 例題2 同じ半径を持つ円と扇形を比べることで、中心角を求めるという考え方です。 半径が9㎝の円の円周の長さは、\(2\times \pi\times 9=18\pi(cm)\) 半径が9㎝の扇形の弧の長さは、問題文より \(3\pi(cm)\) です。扇形 A = 面積 L = 円周の長さ R = 半径 扇形 A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 弓形 A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 円




Study 円錐の側面 扇形 の中心角の求め方 中2数学 ちくらっぽインク




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear
・平行四辺形の面積(2辺と間の角度) 2辺とその間の角度から平行四辺形の面積を計算します。 ・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算します。 円・扇形の面積 ・円の面積 半径から円の面積と周囲の長さを計算します。扇形の面積 A m 2 扇形の角度 θ ° 扇の半径 r m 扇形の面積 A m 2 扇形の角度 θ rad 扇の半径 r m 円弧の長さ l m 扇形の角度 θ ° 扇の半径 r m 円弧の長さ l m 扇形の角度 θ rad 扇の半径



半径4cm面積6pcm の扇形の中心角の求め方を教えてください Yahoo 知恵袋
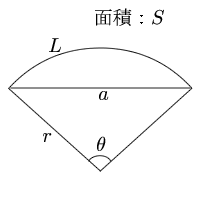



扇形 面積の計算 計算サイト




扇形 周の長さの求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




扇形の弧の長さの求め方 公式と計算例




中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




Kelas 7 Catatan Tentang 中1 数学 範囲 Clear



3
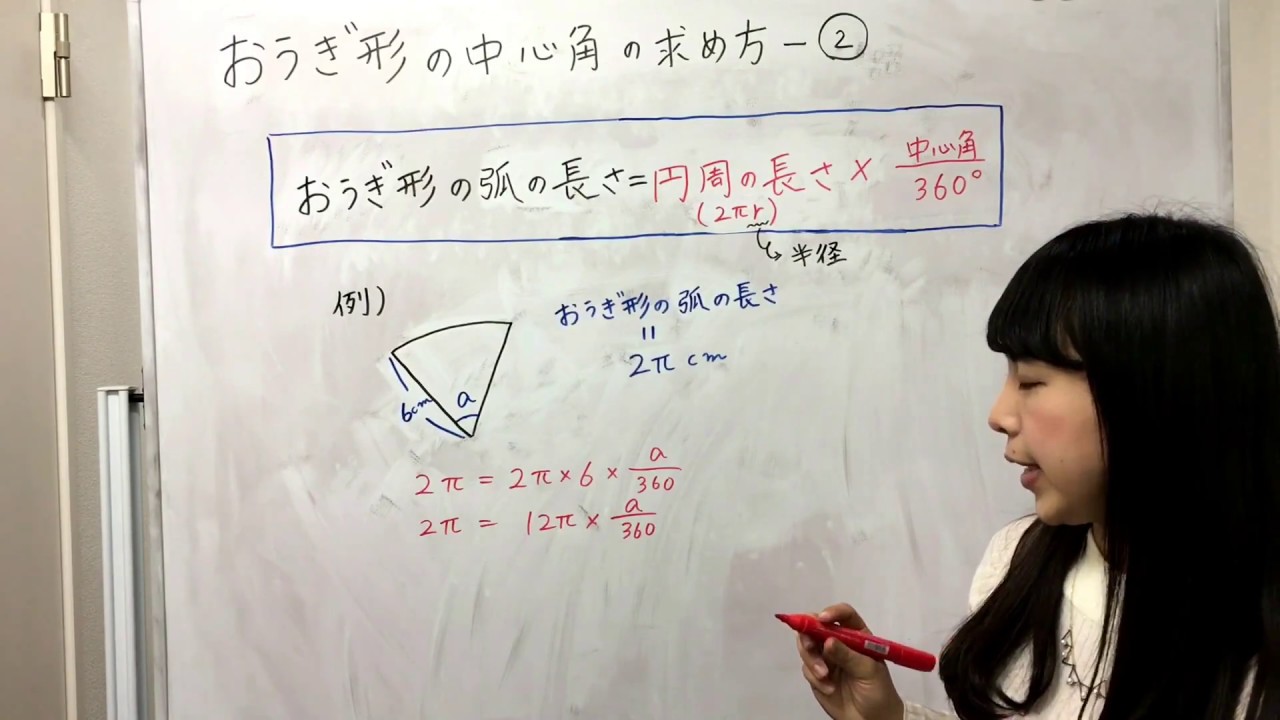



おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト
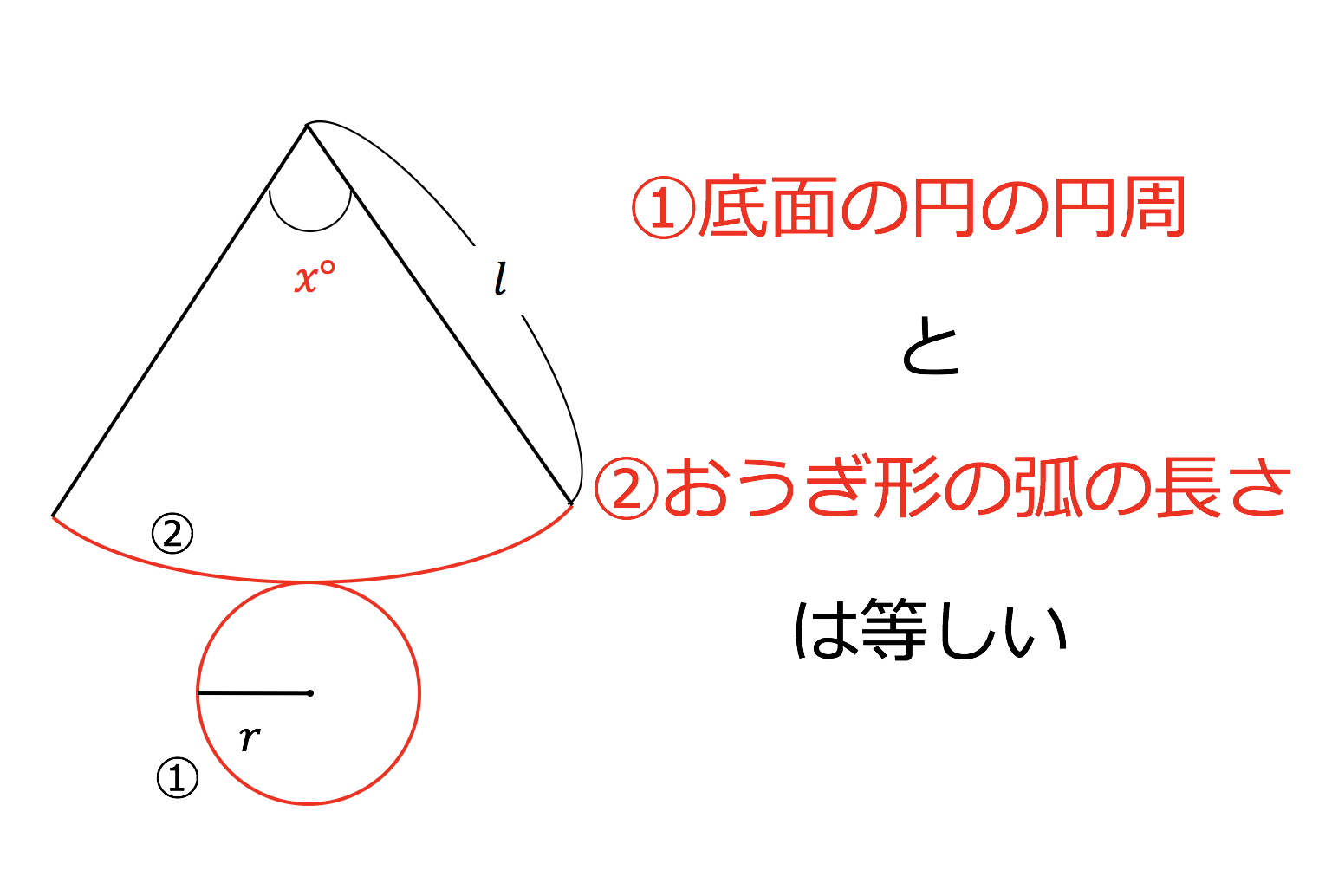



3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



1




扇形の弧の長さの求め方 公式と計算例



数学の公式集 No 003 幾何図形 扇形の面積と円弧の長さ




おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ




円 扇形 の面積 周や弧の長さの公式 数学fun




扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア




おうぎ形の中心角の求め方 Youtube




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




円錐の側面積 展開図の扇形の中心角 半径 母線を軸として解く 身勝手な主張




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




扇形の中心角の求め方を教えてください Clear




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




裏技 おうぎ形の面積を一瞬で求める 弧の長さを利用した裏技公式 中学数学 平面図形 2 Youtube



至急です 扇形の中心角の求め方を教えてください Yahoo 知恵袋




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ



弧度法ってなんだよ ラジアンってなんだよ ってなっている君へ 動画解説あり




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月




おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に




扇形の中心角の求め方 面積と半径がわかっているパターン Youtube



3




角度 Wikipedia



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ



至急 扇形の中心角の求め方 小学生 ママの交流掲示板 ママスタコミュニティ




おうぎ形の中心角の求め方を教えて下さい Clear




中1 数学 空間図形9 おうぎ形の公式 17分 Youtube




扇形や円の問題と図形の回転移動 駒澤塾 中学受験の算数 理科



円と扇形 中学受験ー算数解き方ポータル




3の扇形の中心角が90度になる理由を教えてください 3の扇形の中心角が 中学校 教えて Goo




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




弧度法とは 度数法との違いと表 求め方 理系ラボ




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube




中1です お願いがあります 扇形の中心角の求め方を Clear



1




公式を図解 すい体の体積 円すいの表面積の求め方
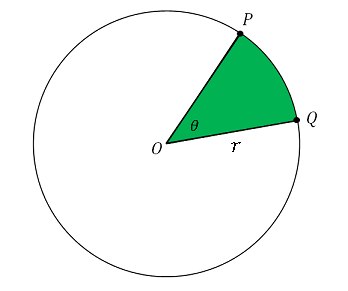



扇形の弧の長さと面積




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
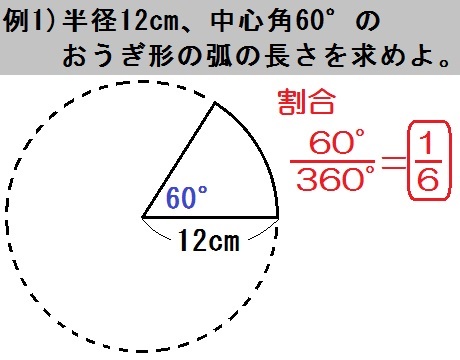



中学数学 平面図形 のコツ 円とおうぎ形




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




半径6cm 面積18pcm の扇形の中心角の求め方を教えて欲しいです Clear




1分でわかる 扇形の中心角の求め方 Youtube




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト
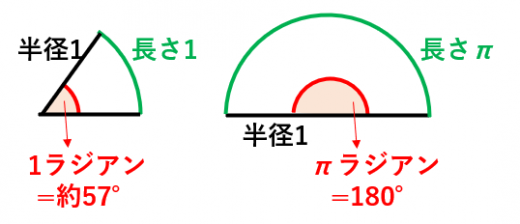



弧度法の意味と度数法に対するメリット 高校数学の美しい物語




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題
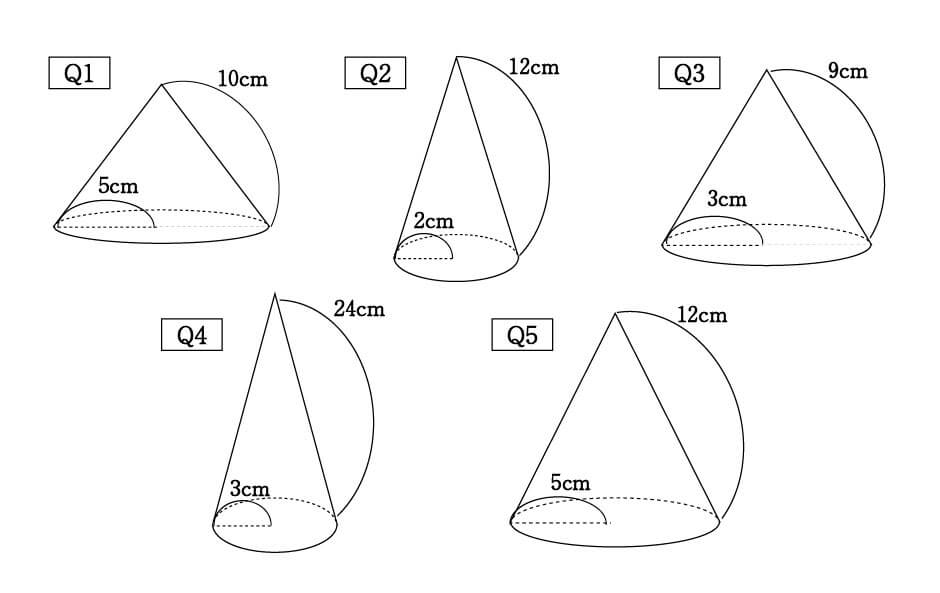



数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく




標準 おうぎ形と正方形の面積 なかけんの数学ノート




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち



扇形の面積は 1分でわかる意味 公式 求め方 ラジアンとの関係



中心角40度 弧の長さ2pcmの扇形の面積中心角30度 弧の長さpcmの扇形 Yahoo 知恵袋




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく




弧度法で扇型のいろいろな計算が簡単に 高校数学の知識庫




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
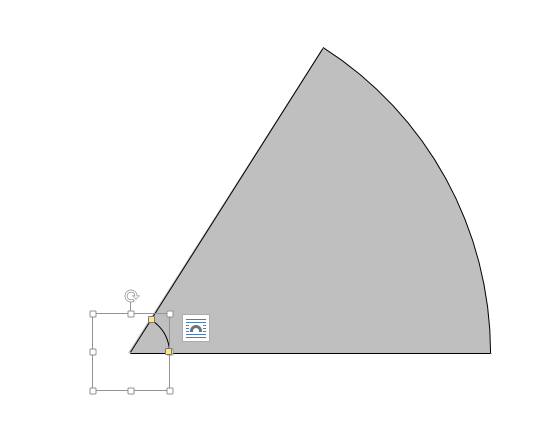



Wordで扇形を作成 中心角の設定は 数学教材で使える画像の作り方は 数スタ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿