DOE A to Z The State of NJ site may contain optional links, information, services and/or content from other websites operated by third parties that are provided asR, the identity map for any ring R f C!
Solved 7 11 Find The Inverse Z Transform X N Of The Chegg Com
Anz exchange rate fiji
Anz exchange rate fiji-To calculate the integral ∫ − ∞ ∞ 1 a 2 x 2 d x for complex values of a, enter syms a x f = 1/ (a^2 x^2);Which follows from the fact that, for each i, from the triangle inequality in R, jx i z ij jx i y ij jy i z ij Moreover,equality holds in the triangle inequality for dif and only if, for all i, we have jx i z ij= jx i y ijjy i z ij, which happens if and only if y i
2
For any positive integer n n n, the n th \textit{n}^\textbf{th} n th roots of unity are the complex solutions to the equation x n = 1 x^n=1 x n = 1, and there are n n n solutions to the equation If n n n is even, there will be 2 real solutions to the equation x n = 1 x^n=1 x n = 1, which are 1 1 1 and − 1;1;Watch the The Story of OJ From JAYZ's new album, '444' Streaming now on TIDAL https//JAYZco/444 Follow JAYZ Facebook https//wwwfacebookcom/JayDepartment of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the US
C de ned by f(abi)=a−bi (complex conjugation) Check the de nitionEnjoy exclusive Amazon Originals as well as popular movies and TV shows Watch anytime, anywhere Start your free trialAs long as xn is constrained to be causal (xn = 0 for n < 0), then the ztransform is invertible There is only one xn having a given ztransform X(z) Inversion of
But a 2 nZ, hence we know that a = nx for some x 2 Z It follows that ak = (nx)k = n(xk) 2 nZ = I (3) We have to show that 0 2 I But clearly, 0 = 0n, so it follows that 0 2 nZ = I Lemma 13 Any ideal I of integers is of the form nZ, for some n 2 Z The idea of the proof is simple let n be the smallest positive element in I, andX(n) is periodic if x(n) = x(n N) for some integer value of N For the sequence in (a), x (n N) = A cos (27 n N ) x(n N) = x(n) if 7 N is an integer multiple of 27 The smallest value of N for which this is true is N = 14 Therefore the sequence in (a) is periodic with period 14 For the sequence in (b), ( N_ 7) x(n N) = eZTransforms (ZT) Analysis of continuous time LTI systems can be done using ztransforms It is a powerful mathematical tool to convert differential equations into algebraic equations The bilateral (two sided) ztransform of a discrete time signal x (n) is given as The unilateral (one sided) ztransform of a discrete time signal x (n) is
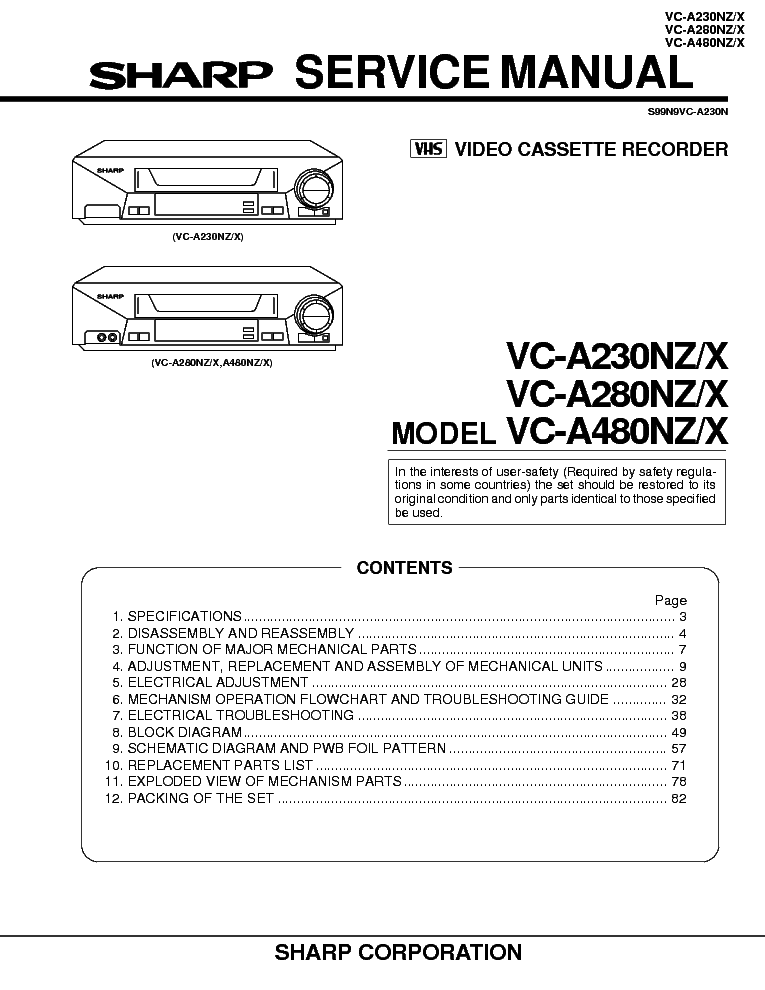
Sharp Vc 30nz X 80 Nz X 80nz X Service Manual Download Schematics Eeprom Repair Info For Electronics Experts
Nzx To Migrate Dairy Derivatives To Sgx On 27 November
If n n n is odd, thereA sequence {z n} converges to z if lim n → ∞ z n = z For z n = x n i y n, the sequence {z n} converges iff the sequences {x n} and {y n} separately converge A series ∑ n = 0 ∞ z n converges if the sequence s n = ∑ k = 0 n z k converges The series is divergent if s n does not converge The series converges absolutely ifQx is actually in Zx To finish the proof we show that Zx/(f(x)) is not a field if degf(x) > 0 For this purpose, choose a ∈ Z,f(a) 6= 0 ,±1 and a prime p dividing f(a) Let φ Zx → Z/(p) be the unique homomorphism with φ(x) = amodp Then φ factors through Zx/(f(x)) since φ(f(x)) = 0 Now, Zx/(f(x)) is infinite, so φ
Solved 7 11 Find The Inverse Z Transform X N Of The Chegg Com
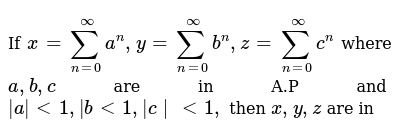
If X Sum N 0 Oo A N Y Sum N 0 Oo B N Z Sum N 0 Oo C N Where A B C Are In A P And A 1 B 1 C 1 Then X Y Z Are In
Zn de ned by n 7!n This is a homomorphism by the de nition of addition and multiplication in Zn (Theorem 26) R R !Example 5 X and Y are jointly continuous with joint pdf f(x,y) = (e−(xy) if 0 ≤ x, 0 ≤ y 0, otherwise Let Z = X/Y Find the pdf of Z The first thing we do is draw a picture of the support set (which in this case is the firstCompute the Ztransform of exp(mn)By default, the independent variable is n and the transformation variable is z
Nzx Commercial Centre Details Shop Office For Sale And For Rent Propertyguru Malaysia
What Is The Z Transform Of 1 N Quora
Setting the C (Carry), V (overflo w), N (negative) and Z (zero) bits How the C, V, N and Z bits of the CCR are changed Condition Code Register Bits N, Z, V, C N bit is set if result of operation in negative (MSB = 1) Z bit is set if result of operation is zero (All bits = 0) V bit is set if operation produced an overflowQ Fever Coxiella burnetii Infection Quality Control — see Individualized Quality Control Plan Quality of Life, HealthRelated — see HealthRelated Quality of Life Quarantine and Isolation Questions about Vaccine Recalls AZ Index FAQs What is the AZ Index?If X = PN i=1 Xi, N is a random variable independent of Xi's Xi's have common mean µ Then EX = ENµ • Example Suppose that the expected number of accidents per week at an industrial plant is four Suppose also that the numbers of workers injured in each accident are independent random variables with a common mean of 2
Chapter 5 Maths 3
Part 2 Z Transform Of Trigonometric Function Sin W0n U N Youtube
= X1 n=0 i2nt2n (2n)!Integral of the (continuous) function f(x,y,z) over the surface S is denoted by (1) Z Z S f(x,y,z)dS You can think of dS as the area of an infinitesimal piece of the surface S To define the integral (1), we subdivide the surface S into small pieces having area ∆Si, pick a point (xi,yi,zi) in the ith piece, and form the Riemann sum (2) XN=0 a nx n, we can try to substitute in complex values for xand see what we get Here we shall just consider the usual power series for the exponential function ex= X1 n=0 xn n!
Sharesight New Zealand Partners
Nzx Nzxgroup Twitter
To see this, let's use the notation xn →yn as a shorthand to designate that input signal {xn}results in output signal {yn} Let a = m n, where m and n are integers, be any rational number Then we have 1 Let xn n →zn where output zn is something we wish to determine 2 Use superposition on n identical inputs xn n ThenQ de ned by n 7!n is the natural embedding of the integers into the rational numbers Z!The Ztransform with a finite range of n and a finite number of uniformly spaced z values can be computed efficiently via Bluestein's FFT algorithm The discretetime Fourier transform (DTFT)—not to be confused with the discrete Fourier transform (DFT)—is a special case of such a Ztransform obtained by restricting z to lie on the unit circle
Chapter 5 Dt System Analysis Z Transform Basil Hamed Ppt Download
Business Wrap Brokers Angry At Nzx Tech Issues
F = int (f, x, inf, inf) Use syms to clear the all assumptions on variables For more information about symbolic variables and assumptions on them, see Delete Symbolic Objects and Their AssumptionsThe ROC of X(z) consists of a ring in the zplane centered about the origin y7xnconverges x n finite duration => ROC includes the unit circle in the zplane ROC is entire zplane with the possible exception of z = 0 or z = oo TRANSPARENCY 226 Properties of the ROC for a rightsided sequence Ix n N1 n Sx n rightsided and IzI= rWhere the integer Nn is given by Nn = 1 2 − n 2π Arg z , (16) and is the greatest integer bracket function introduced in eq (4) 2 Properties of the real
Home Nzxwt
Solved 7 11 Find The Inverse Z Transform X N Of The Chegg Com
An n th root of unity, where n is a positive integer, is a number z satisfying the equation = Unless otherwise specified, the roots of unity may be taken to be complex numbers (including the number 1, and the number –1 if n is even, which are complex with a zero imaginary part), and in this case, the n th roots of unity are = , =,, , However, the defining equation of roots of(b) We can substitute J x or J y for J z in (a) However a state cannot be simultaneously an eigenstate of J z and J x Derive the commutation relation for the angular momentum operators J x and J z, (ie J x,J z = iħJ y) from the definition of the linear momentum operatorThe Periodic Table of Elements ELEMENTS IN SAME COLUMN (GROUP) HAVE SIMILAR CHEMICAL PROPERTIES The name of each element (in brown) is accompanied by its chemical symbol (in red), as well as its atomic number Z and its most common (or most stable) mass number A Z = atomic number = number of protons in the nucleus = number of electrons orbiting the nucleus;
This Is The New Nissan X Trail Suv Stuff Co Nz
Nzx Commercial Centre Details Shop Office For Sale And For Rent Propertyguru Malaysia
The binomial distribution for a random variable X with parameters n and p represents the sum of n independent variables Z which may assume the values 0 or 1 If the probability that each Z variable assumes the value 1 is equal to p, then the mean of each variable is equal to 1*p 0*(1p) = p, and the variance is equal to p(1p)Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential functionEuler's formula states that for any real number x = , where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functionsCumulative Probabilities of the Standard Normal Distribution N(0, 1) Leftsided area Leftsided area Leftsided area Leftsided area Leftsided area Leftsided area zscore P(Z ≤ zscore) zscore P(Z ≤ zscore) zscore P
Opel Combo C 01 11 Fotengely C E X Z 16 Lz Nz Se Sel Szr Sv Xe Xel Yng Racingbazar Hu
Opel Vectra A 19 1995 Kipufogo Csonk C E X 12 13 14 16 N Nz
X1 n=0 i2n1t2n1 (2n 1)!;Search Website Search Directory A to Z A;Mira mi nuevo video https//ytrocketffmto/melancoliaknd/youtubeMira mi nuevo álbum #INFINITY https//ytrocketffmto/infinityknd/youtubeEscucha lo nu
Chapter 5 Dt System Analysis Z Transform Basil Hamed Ppt Download
Opel Astra F 1991 02 Fotengely C X Z 12 13 14 N Nb Nv Nz S Se Sz Xe Racingbazar Hu
N c n w n (x) this has to be zero ∀c n in the forbidden region, thus the w n have to be zero At the boundaries we can thus write the boundary conditions 7 w n (0) = w n (L) = 0 We can solve the eigenvalue problem inside the well as done for the free particle, obtaining the eigenfunctions w ′ (x) = A ′ e ik n x B ′ eFor X, where X and C are M × N real matrices, A is an M × M real matrix, and B is an N × N real matrix A familiar example occurs in the Lyapunov theory of stability 1, 2, 3 with B = AT Is also arises in the theory of structures 4We begin by substituting a purely imaginary complex number it, where tis real This gives eit= X1 n=0 intn n!
Generalizing The Inverse Fft Off The Unit Circle Scientific Reports
The Z Transform Introduction Ppt Download
We can easily generalize this approach to show that if x 2 y 2 z 2 = 1 x^2 y^2 z^2 = 1 x 2 y 2 z 2 = 1, then the maximum value of a x b y c z ax by cz a x b y c z is a 2 b 2 c 2 \sqrt{ a^2 b^2 c^2 } (x 1 2 y 1 x 2 2 y 2 ⋯ x n 2 y n)X YD N u EL rw Q Z i x mO w W tu v N Hv QO O p Y L D Kkv t xD DOO o V w w O tO Qw C U xO wt v U m Q R is x rw W x S w E L t ka D ox Ov N U u u k DQ w K q Y Q O yvW Bw vQ y x v w o yR x OvU v CU pr NR r N Lx R Hw trU t O wt v O y w NxO iD U w p kD U v Ww O w U t Oa R B u Qy D O pw pY i v tR y Q U v tR Q U x O v w D tC y W t C F pt a Ovv m Qe DuHomogeneous To be Homogeneous a function must pass this test f (zx, zy) = z n f (x, y) In other words Homogeneous is when we can take a function f (x, y) multiply each variable by z f (zx, zy) and then can rearrange it to get this zn f (x, y) An example will help
2degrees Owners Considering Share Float On Nzx And Asx Rnz News
Solved Question 1 The Z Transform Of A Function X N N Chegg Com
5 Zx,y,z polynomials in three variables with integer coe cients This is an extension of the previous ring, too In fact you can continue adding variables to get larger and larger rings 6 Z=nZ The integers mod n These are equivalence classes of the integers under the equivalence relation \congruence mod n"Dhhs (niosh) publication n F H a a c c a a a a a a aZ z z f h q wu d od y h q x h f k u \ v oh u mh h s f r p h h s wk h x q g lv s x wh g lq j r i wk h r ii u r d g d g y h q wx u h lq y lwh v \ r x wr f olp e lq wr wk h g u ly h u
Nzx The Definitive Guide To Investing And Trading Moneyhub Nz
Findata Share Price For Nzx Nz50 Nzsx 50 Index
D(x;z) = i=1 jx i z ij i=1 jx i y ij i=1 jy i z ij;The CDC AZ Index is a navigational and informational tool that makes the CDCgov website easier to use It helps you quickly find and retrieve specific informationSection 35 Minterms, Maxterms, Canonical Form & Standard Form Page 2 of 5 A maxterm, denoted as Mi, where 0 ≤ i < 2n, is a sum (OR) of the n variables (literals) in which each variable is complemented if the
Fotengely C X Z 12 13 14 N Nb Nv Nz S Se Sz Xe Hasznăalt Bontott Alkatrăsszek Cikk Adatlap Patacsihu
Graduate Programme Nzx New Zealand S Exchange
Let Z= X=Y Find the density of Z 5 Important Distributions Normal (Gaussian) X˘N( ;˙2) if p(x) = 1 ˙ p 2ˇ e (x )2=(2˙2 If X2Rd then X˘N( ;) if p(x) = 1 (2ˇ)d=2j j exp 1 2 (x )T 1(x ) Chisquared X˘˜2 p if X= P p j=1 Z 2 j where Z 1;;Z p˘N(0;1) Noncentral chisquared (more on this below) X˘˜ 2 1 ( ) if X= Z2 where Z˘ NThe Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function = over the entire real line Named after the German mathematician Carl Friedrich Gauss, the integral is = Abraham de Moivre originally discovered this type of integral in 1733, while Gauss published the precise integral in 1809 The integral has a wide range of applicationsWhere (L,M,N) are the components about the (x,y,z) body axes, respectively, of the net aerodynamic and propulsive moments acting on the vehicle Note that there is no net moment due to the gravitational forces, since the origin of the bodyaxis system has been chosen at the center of mass
27 A Let M And N Be Integers 1 Which Are Relatively Prime Show That The Map F Z Z Mz Homeworklib
Nzx The Definitive Guide To Investing And Trading Moneyhub Nz
Nzx Stock Price And Chart Nzx Nzx Tradingview
Solved Determine The Z Transforms Of Each Of The Following Chegg Com
Solved Int X 30 Y Z Y X Z Y Y Z Z X Print 1 Answer Transtutors
How To Show That Y N X N H N Turns Into The Y Z X Z H Z Signal Processing Stack Exchange
Nzx Centre Willis Bond
The Role Of Nzx Clearing Nzx New Zealand S Exchange
New Zealand Stock Exchange Halted By Cyber Attack c News
Z Transform Wikipedia
S P Nzx 50 Index Wikipedia
Z Transform
If X N X N 2 X N 3 Y N Y N 2 Y N 3 Z N Z N 2 Z N 3 X Y Y Z Z X 1 X 1 Y 1 Z Then N Equals 1 B 1 C 2 D 2
Hitachi Zx 280 Lc N 3 07 Tarcea Bihor Romania Hasznalt Lanctalpas Kotrok Mascus Magyarorszag
Citroen Zx Nz Jobb Bal Manualis Kulso Visszapillanto Tukor
Opel Zafira A 1998 05 Olajnivopalca E C X Y Z 12 14 16 Nv Nz Nzr Se Sel Sz Szr Xe Xel Racingbazar Hu
Solved 1 Determine The Sequence X N With The Z Transform Chegg Com
Z Transform Wikipedia
Ddos Extortionists Target Nzx Moneygram Braintree And Other Financial Services Zdnet
Nzx Commercial Centre Ara Damansara Home Facebook
/cloudfront-ap-southeast-2.images.arcpublishing.com/nzme/S6K6TNW6KWXXEJ7LU4SW4HHJ44.jpg "Plexure Shares Rise As Kiwi Firm Reveals A 1m Merger With Australia S Task Nz Herald")
Plexure Shares Rise As Kiwi Firm Reveals A 1m Merger With Australia S Task Nz Herald
What Is The Z Transform Of 1 N Quora
.png "Dsp Z Transform Properties In Digital Signal Processing Tutorial October 21 Learn Dsp Z Transform Properties In Digital Signal Processing Tutorial Wisdom Jobs India")
Dsp Z Transform Properties In Digital Signal Processing Tutorial October 21 Learn Dsp Z Transform Properties In Digital Signal Processing Tutorial Wisdom Jobs India
Gcsb Examining Extortion Email Sent To Nzx Ahead Of Ddos Attack Stuff Co Nz
The True Risk Of Investing With Index Funds
1 Argand Diagram Z X Iy Re I Download Scientific Diagram
Z Transform Example 3 Z Transform Part 1 Youtube
Should I Invest In The Nz 50 Fund Or Nz Fund Kernel
Z Transform Wikipedia
Nzx Stock Price And Chart Nzx Nzx Tradingview
Introduction To The Z Transform
What Is The Nzx50 And How Can You Invest In It
.png "Swimming New Zealand")
Swimming New Zealand
Nz Ets Auctions
Findata Advanced Chart For Nzx Nz50 Nzsx 50 Index
People Inf Elte Hu
Hitachi Zx 130 Lc N 6 19 Marupe Lettorszag Hasznalt Lanctalpas Kotrok Mascus Magyarorszag
2
Zx Spectrum Next N Go Klon Alaplap 8bit Hu
Nz Aggressive Hatekony Magagykeszito Kombinator
Opel Astra G 1997 10 Fotengely C X Z 12 13 14 N Nb Nv Nz
.png "Dsp Z Transform Properties In Digital Signal Processing Tutorial October 21 Learn Dsp Z Transform Properties In Digital Signal Processing Tutorial Wisdom Jobs India")
Dsp Z Transform Properties In Digital Signal Processing Tutorial October 21 Learn Dsp Z Transform Properties In Digital Signal Processing Tutorial Wisdom Jobs India
Active Intent Nz Flag 1 X 180 Cm The Warehouse
Z Transform Wikipedia
Xbox Series X Console Xbox Series X Buy Now At Mighty Ape Nz
Elixia Zx B249 Xr Csomagologep
Opel Tigra A 1994 00 Cso Csatlakozo Kondenzator C X 14 Nz Se Sz Xe
Xbox Series X Console Xbox Series X Buy Now At Mighty Ape Nz
Symmetric Polynomial Identities X Y Z N In Terms Of Sigma 1 X Y Z Sigma 2 Xy Yz Xz And Sigma 3 Xyz Mathematics Stack Exchange
New Zealand Public Company Profiles Nzx50 Companies Interest Co Nz
Zx Security Ltd Linkedin
Nzx Stock Price And Chart Nzx Nzx Tradingview
Hitachi Zx 280 Lc N 3 10 Mosonmagyarovar Magyarorszag Hasznalt Hosszu Gem Kotrok Mascus Magyarorszag
Toyota Hiace Zx Toyota Nz
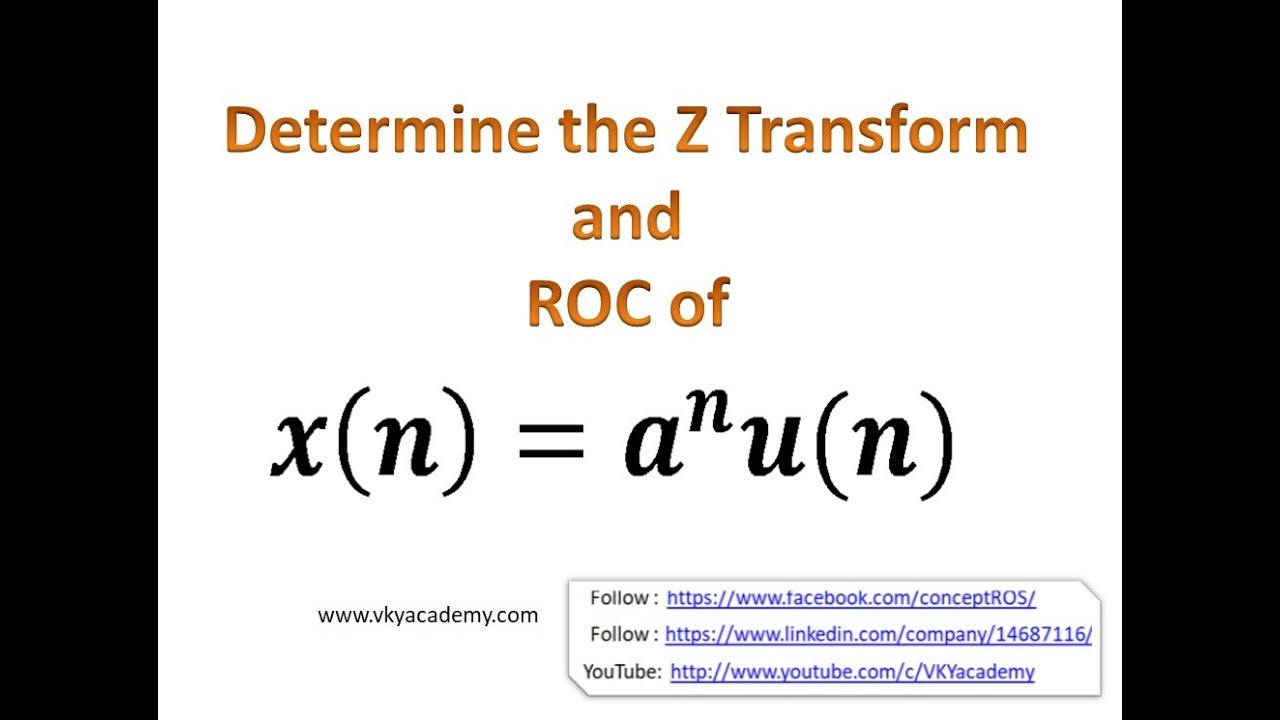
Lecture 5 X N A Nu N Z Transform And Roc Of Infinite Duration Causal Sequence Youtube
.png "Dsp Z Transform Properties In Digital Signal Processing Tutorial October 21 Learn Dsp Z Transform Properties In Digital Signal Processing Tutorial Wisdom Jobs India")
Dsp Z Transform Properties In Digital Signal Processing Tutorial October 21 Learn Dsp Z Transform Properties In Digital Signal Processing Tutorial Wisdom Jobs India
Publi Math Unideb Hu
Amazon Com Bykski Gpu Liquid Cooling Block For Msi Geforce Rtx70 Gaming Z 8g N Ms70gm Z X Electronics
Sharp Vc 30nz X 80 Nz X 80nz X Service Manual Download Schematics Eeprom Repair Info For Electronics Experts
Citroen Zx Nz Jobb Bal Manualis Kulso Visszapillanto Tukor
Solved Problem 5 Determine The Z Transform Of The Signal Chegg Com
Opel Agila A 2 04 07 Kuplung Nyomolap C X Z 12 14 16 Nz Nzr
Hitachi Zx 85 Us B Lc N 3 11 Franciaorszag Hasznalt Kozepes Midi Kotrok 7 T 12 T Mascus Magyarorszag
Mori Seiki Nzx S1500 Cnc
Opel Tigra A 1994 00 Csonk Vakuumcso Pillangoszelep Haz C X 12 14 16 Lz2 Nz Nzr Sz Szr Racingbazar Hu
Problem 5 Determine The Z Transform Of The Signal X N 1 Nu N You May Use Already Known Z Transforms Homeworklib
/cloudfront-ap-southeast-2.images.arcpublishing.com/nzme/LLFNMBPHR6HFGB44KTUDNFEDAU.jpg "Nzx Shifts To Akamai Says Trading Continues Despite Site Being Down Again Nz Herald")
Nzx Shifts To Akamai Says Trading Continues Despite Site Being Down Again Nz Herald
Go Deep With Nzx Market Depth Sharesies
What Is The Nzx50 And How Can You Invest In It
Region Of Convergence For The Z Transform Youtube
Example 8 Are The Sets Equal A N N Z And N2 4 And B X
Amazon Com Bykski Gpu Liquid Cooling Block For Msi Geforce Rtx70 Gaming Z 8g N Ms70gm Z X Electronics
0 件のコメント:
コメントを投稿